Check if a Parentheses String Can Be Valid

Problem

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

It is ().
It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
It can be written as (A), where A is a valid parentheses string.

You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of '0's and '1's. For each index i of locked,

If locked[i] is '1', you cannot change s[i].
But if locked[i] is '0', you can change s[i] to either '(' or ')'.

Return true if you can make s a valid parentheses string. Otherwise, return false.

Example 1:

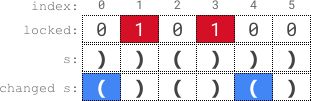
Input: s = "))()))", locked = "010100"
Output: true
Explanation: locked[1] == '1' and locked[3] == '1', so we cannot change s[1] or s[3].
We change s[0] and s[4] to '(' while leaving s[2] and s[5] unchanged to make s valid.

Example 2:

Input: s = "()()", locked = "0000"
Output: true
Explanation: We do not need to make any changes because s is already valid.

Example 3:

Input: s = ")", locked = "0"
Output: false
Explanation: locked permits us to change s[0]. 
Changing s[0] to either '(' or ')' will not make s valid.

Constraints:

n == s.length == locked.length
1 <= n <= 10^5
s[i] is either '(' or ')'.
locked[i] is either '0' or '1'.

Solution (Java)

class Solution {
    public boolean canBeValid(String s, String locked) {
        if (s == null || s.isEmpty()) {
            return true;
        }
        if ((s.length() & 1) > 0) {
            return false;
        }
        if (locked == null || locked.isEmpty()) {
            return true;
        }
        int numOfLockedClose = 0;
        int numOfLockedOpen = 0;
        for (int i = 0; i < s.length(); i++) {
            int countOfChars = i + 1;
            if (s.charAt(i) == ')' && locked.charAt(i) == '1') {
                numOfLockedClose++;
                if (numOfLockedClose * 2 > countOfChars) {
                    return false;
                }
            }
            int j = s.length() - 1 - i;
            if (s.charAt(j) == '(' && locked.charAt(j) == '1') {
                numOfLockedOpen++;

                if (numOfLockedOpen * 2 > countOfChars) {
                    return false;
                }
            }
        }
        return true;
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).