1739. Building Boxes

Problem

You have a cubic storeroom where the width, length, and height of the room are all equal to n units. You are asked to place n boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:

• You can place the boxes anywhere on the floor.

• If box x is placed on top of the box y, then each side of the four vertical sides of the box y must either be adjacent to another box or to a wall.

Given an integer n, return** the minimum possible number of boxes touching the floor.**

  Example 1:

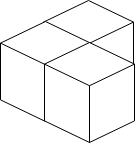
Input: n = 3
Output: 3
Explanation: The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 2:

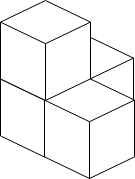
Input: n = 4
Output: 3
Explanation: The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 3:

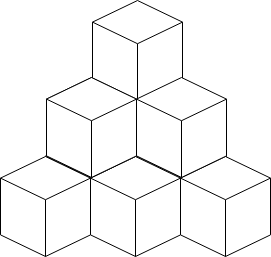
Input: n = 10
Output: 6
Explanation: The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.

  Constraints:

• 1 <= n <= 10^9

Solution

class Solution {
    static final double ONE_THIRD = 1.0d / 3.0d;

    public int minimumBoxes(int n) {
        int k = findLargestTetrahedralNotGreaterThan(n);
        int used = tetrahedral(k);
        int floor = triangular(k);
        int unused = (n - used);
        if (unused == 0) {
            return floor;
        }
        int r = findSmallestTriangularNotLessThan(unused);
        return (floor + r);
    }

    private int findLargestTetrahedralNotGreaterThan(int te) {
        int a = (int) Math.ceil(Math.pow(product(6, te), ONE_THIRD));
        while (tetrahedral(a) > te) {
            a--;
        }
        return a;
    }

    private int findSmallestTriangularNotLessThan(int t) {
        int a = -1 + (int) Math.floor(Math.sqrt(product(t, 2)));
        while (triangular(a) < t) {
            a++;
        }
        return a;
    }

    private int tetrahedral(int a) {
        return (int) ratio(product(a, a + 1, a + 2), 6);
    }

    private int triangular(int a) {
        return (int) ratio(product(a, a + 1), 2);
    }

    private long product(long... vals) {
        long product = 1L;
        for (long val : vals) {
            product *= val;
        }
        return product;
    }

    private long ratio(long a, long b) {
        return (a / b);
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).