Problem
You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.
Given the integer n, return **the number of *complete rows* of the staircase you will build**.
Example 1:
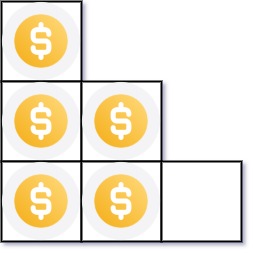
Input: n = 5
Output: 2
Explanation: Because the 3rd row is incomplete, we return 2.
Example 2:
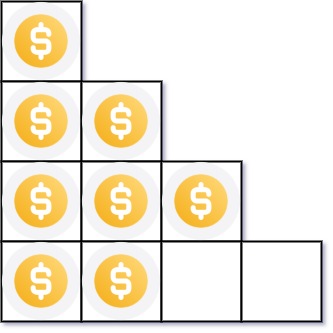
Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.
Constraints:
1 <= n <= 2^31 - 1
Solution (Java)
class Solution {
public int arrangeCoins(int n) {
if (n < 0) {
throw new IllegalArgumentException(
"Input Number is invalid. Only positive numbers are allowed");
}
if (n <= 1) {
return n;
}
if (n <= 3) {
return n == 3 ? 2 : 1;
}
// Binary Search space will start from 2 to n/2.
long start = 2;
long end = n / 2;
while (start <= end) {
long mid = start + (end - start) / 2;
long coinsFilled = mid * (mid + 1) / 2;
if (coinsFilled == n) {
return (int) mid;
}
if (coinsFilled < n) {
start = mid + 1;
} else {
end = mid - 1;
}
}
// Since at this point start > end, start will start pointing to a value greater
// than the desired result. We will return end as it will point to the correct
// int value.
return (int) end;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).