1478. Allocate Mailboxes

Problem

Given the array houses where houses[i] is the location of the ith house along a street and an integer k, allocate k mailboxes in the street.

Return **the *minimum* total distance between each house and its nearest mailbox**.

The test cases are generated so that the answer fits in a 32-bit integer.

  Example 1:

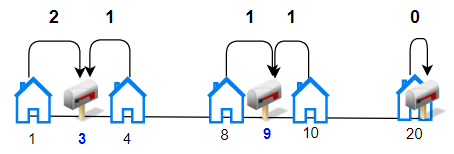
Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 

Example 2:

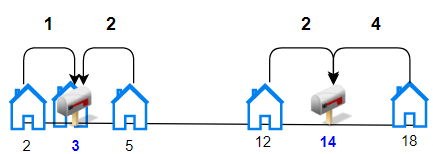
Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

  Constraints:

• 1 <= k <= houses.length <= 100

• 1 <= houses[i] <= 10^4

• All the integers of houses are unique.

Solution

class Solution {
    public int minDistance(int[] houses, int k) {
        Arrays.sort(houses);
        int n = houses.length;
        int[][] dp = new int[n][k + 1];
        for (int[] ar : dp) {
            Arrays.fill(ar, -1);
        }
        return recur(houses, 0, k, dp);
    }

    private int recur(int[] houses, int idx, int k, int[][] dp) {
        if (dp[idx][k] != -1) {
            return dp[idx][k];
        }
        if (k == 1) {
            int dist = calDist(houses, idx, houses.length - 1);
            dp[idx][k] = dist;
            return dp[idx][k];
        }
        int min = Integer.MAX_VALUE;
        for (int i = idx; i + k - 1 < houses.length; i++) {
            int dist = calDist(houses, idx, i);
            dist += recur(houses, i + 1, k - 1, dp);
            min = Math.min(min, dist);
        }
        dp[idx][k] = min;
        return min;
    }

    private int calDist(int[] ar, int start, int end) {
        int result = 0;
        while (start < end) {
            result += ar[end--] - ar[start++];
        }
        return result;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).