Problem
Given two binary search trees root1 and root2, return **a list containing all the integers from both trees sorted in *ascending* order**.
Example 1:
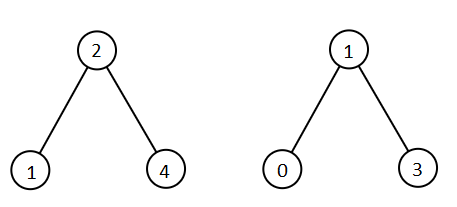
Input: root1 = [2,1,4], root2 = [1,0,3]
Output: [0,1,1,2,3,4]
Example 2:
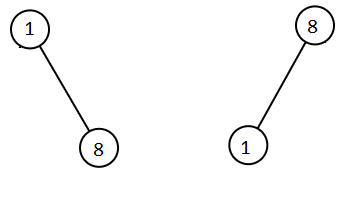
Input: root1 = [1,null,8], root2 = [8,1]
Output: [1,1,8,8]
Constraints:
The number of nodes in each tree is in the range
[0, 5000].-10^5 <= Node.val <= 10^5
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
List<Integer> list1 = getAllNodes(root1);
List<Integer> list2 = getAllNodes(root2);
List<Integer> merged = new ArrayList<>();
merged.addAll(list1);
merged.addAll(list2);
Collections.sort(merged);
return merged;
}
private List<Integer> getAllNodes(TreeNode root) {
List<Integer> list = new ArrayList<>();
return inorder(root, list);
}
private List<Integer> inorder(TreeNode root, List<Integer> result) {
if (root == null) {
return result;
}
inorder(root.left, result);
result.add(root.val);
return inorder(root.right, result);
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).